本日説明すること
こんにちは。儲かるデザインの佐藤です。
私の周りでpythonなどのプログラミング言語を使った売上分析をはじめる企業様が増えています。
当社のコンサルティングサービスでも機械学習を使った分析を求められるシーンが増えていました。
本日は時系列分析について説明いたします。
まず時系列分析とは、時間の経過に伴い変化するデータを分析することです。
何を予測するかといえば売上や株価や血圧など、時間の経過に従って変化する現象を定期的に観測できるものであれば何でも予測できます。
これを読んでいただいている方の多くは売上や利益を予測したいと思っている方が多いかもしれませんね。
売上予測はあくまで理想値。
そんなの当たるはずないから意味ないよ!と思う方も多いでしょう。
たしかに重要なのは目の前の数字を追うことなのは間違いありません。
しかし、計画性の高い経営は多くの場合、収益拡大へと結びつきます。
計画性の高い経営をしたい(または店舗運営をしたい)という方はこれをきっかけに是非、時系列分析を勉強してみてはいかがでしょうか?
タイトルのARMA、ARIMA、SARIMAというのは統計学において時系列データに適用されるモデルのことです。
まずは本題である時系列分析に入る前に、統計学における回帰分析の種類から説明していきましょう。

①線形回帰
②自己回帰(AR)
③移動平均(MA)
④自己回帰移動平均(ARMA)
ARIMA、SARIMAを説明する前に、本日は上記の4つについて簡単に説明させていただこうと思います。
今回、難しい数式は一切使いません。
まずは線形回帰から説明しましょう。
線形回帰
あるお店の売上を予測するとします。
ご存じの方が多いと思いますが、小売業で売上を求めるものに売上=客数×客単価という公式がありますよね。
もし自店の売上が1,000,000円(100万円)だったとするなら、1,000人の客数と1,000円の客単価(1回の購買によって1人当たりが支払う額のこと)に分解できるというものです。
売上100万円=客数1,000人×客単価1,000円
このときの売上を目的係数、客数や客単価を説明係数と言います。
ここで一度、売上と客単価のみに着目してみましょう。
たとえば、客単価が1,000円の時のデータを見ると105万円の売上が上がっていたとします。
続いて客単価が2,000円の時には201万円の売上が上がっていました。
客単価が3,000円の時にはいくら上がるの?という質問をしたら・・・
300万円くらい?
そうですね。
今回は簡単な数字でしたが、数字が複雑な場合は図を描くとわかりやすいかもしれません。
縦軸を売上、横軸を客単価とします。
売上105万の時、客単価1,000円
売上201万の時、客単価2,000円
売上〇〇万の時、客単価は3,000円。
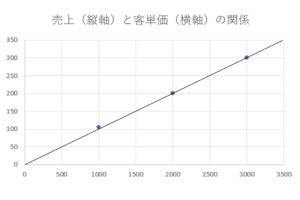
売上と客単価が合わさるポイントに点をつけます。
その点の上に線を引けば右上がりの線ができあがりますね。
この線を回帰直線と言います(曲線であれば回帰曲線)。
このように、売上(目的係数)と客単価(説明係数)の組み合わせをたくさん集めて回帰係数(傾きを示す係数のこと)を求めるのが線形回帰です。
ここで重要なのは誤差。
売上を予測する際には必ず誤差が乗ります。
引いた線の精度を高めるためにはできるだけ誤差を最小にする必要があります。

図のような5つの点がある時、回帰直線(または曲線)に対してどのくらいの誤差が出ているのでしょうか。
誤差の大きさを求めるために、左側から誤差を足して計算してみましょう。
左からズレが0、10、-20、10、0だとすると
0+10-20+10+0=0
誤差ゼロとなっていまいます。
これだけずれていて合計した誤差がゼロというのは納得できませんね。
回帰係数(傾き)はどのように求めるのがベストかというと誤差を最小にする方法【最小二乗法】を使うことになります。
この場合、それぞれの数字を二乗することにより、負の位も正の位にあわせて自然な誤差を算出することができます。
0の二乗、10の二乗、-20の二乗、10の二乗、0の二乗。
0+100+400+100+0=600
これらの誤差を全て足すと600となります。
精度の高い回帰直線(曲線)を引くためには、この誤差を最小にしなければならないということは言うまでもありません。
ここまでの流れを改めて復習すると、線形回帰では売上(目的係数)と客単価(説明係数)の組み合わせをたくさん集めて、できるだけ誤差の少ない回帰係数(傾きを示す係数のこと)を求めることが大切なのです。
次に自己回帰(AR)モデルを説明いたします。
自己回帰(AR)
自己回帰とは今日までの売上から明日の売上を占うというモデルです。
今が9月だとすると8月、7月、6月、5月・・・のデータを集めて9月以降の売上を予測することができます。
要するにここからが時系列分析の勉強です。
最初に勉強した線形回帰との違いは、【線形回帰】が客単価から売上を求めるのに対して、【自己回帰(AR)】は先月までの売り上げから今月以降の売り上げを求めるパターンとなります。
ちなみにどちらでもうまくいかない場合には2つをミックスしたVAR(ベクトル自己回帰)という分析を使うと良いでしょう。
これは先月以前の客単価から今月の客単価を求めるようなものです。
話を自己回帰(AR)に戻しますが、自己回帰モデルでは何か月前までのデータを見るか(pと言われる次数)のハイパーパラメータ設定が非常に重要です。
【今日の話で一番ここが重要で難しい話です。寝ないでくださいね。】
何個前までのデータを参考にするのがベストかという指標にAIC(赤池情報基準)というものがあります。
統計学の世界では非常に有名な指標であり、多くの統計ソフトに備わっているのではないでしょうか。
AICは低いほどよく、AICの値が大きいと過学習と考えられます。
精度の高い時系列分析をするためにはAICで自己回帰(AR)モデルのちょうどいい次数p(何か月前までのデータを見るか)を見つけることがポイントなのです。
【本日一番難しい話はここでおしまい。ふう~疲れた・・・】
次は移動平均(MA)モデルを紹介しましょう。
移動平均(MA)
移動平均とは時系列データを平滑化する手法です。
過去の誤差が現在の値にどれだけ影響しているか調べるため、そのブレを補正するために用います。
一般的にp は自己回帰部分の次数と呼ばれる(本日の一番難しい話を読み返してください)のに対して、移動平均部分の次数(何個前までのデータを見るか)はqと表します。
最後に自己回帰(AR)と移動平均(MA)をかけあわせたモデル、自己回帰移動平均(ARMA)を紹介します。
自己回帰移動平均(ARMA)
一度、ARとMAを復習してみましょう。
自己回帰(AR)モデルは今日までの売上から明日の売上を占うという特徴があります。
移動平均(MA)モデルは時系列のブレを平滑化するという特徴があります。
名前の通り、ここまで勉強した自己回帰と移動平均をミックスしたモデルがARMAモデルです。
実際の時系列データに適用する場合、誤差を最小化するパラメータを探るため、最小の p (ARの次数)および q(MAの次数) を見つけることでよりよい結果が得られることが知られています。
次回はARIMA、SARIMAについて説明いたします