クラスター分析
こんにちは。
mocal designの佐藤です。
本日はクラスター分析について話をしていきます。
え!!!
この時期にクラスターの分析?
興味ある!と思った方。
期待を持たせてしまい、申し訳ございません。
コロナのクラスターを発生させないというような話ではありません。
とは言え、意味としてはそのクラスターと全く関係ない話でもありませんので、これから詳しくご説明します。
本日紹介するクラスター分析とは、近い物同士を集めてグループに分ける方法です。
・顧客の特性を分ける
・商品構成分析
・商圏分け
・ポジショニング分析など。
クラスター分析は小売業、流通業においてもマーケティング戦略として使われることがあります。
なお、クラスター分析は「階層的手法」と「非階層的手法」の2つに分類できます。
階層的手法
階層的手法とは近いデータ同士をまとめていくことで、クラスターを形成する手法です。
お菓子売り場で言えば「ポッキーとコアラのマーチは似ているよね」といった分析です。
ここでは距離が近いもの同士をグループ化します。
階層的手法ではデータを階層にわけて並べるので、視覚的にも判別しやすくなります。
ただし、参考にしたいデータの特徴が多い場合、階層的手法は向きません。
非階層的手法
非階層的手法は近いデータ同士が同じクラスターになるよう全体を分割する手法です。
もう少しわかりやすく言うと、近いサンプルを探すことでクラスターを作成する手法です。
非階層的手法では主にk-means法を使います。
k-means法とは最初にわけたいデータの代表を指定し、各データの重心からの距離をサンプルごとに計算してグループ分けする方法です。
手法を説明しましょう。
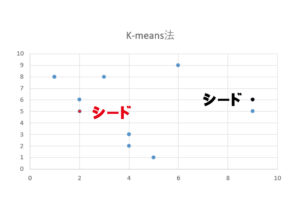
下の図をご覧ください。
ポイントは赤と黒の点です。
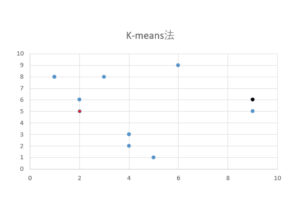
最初に指定する2点をシード(種)と言います。
まずはシードを元にランダムなグループ分けします。
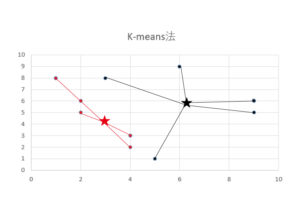
1・各グループに割り当てられた点について、重心を計算します。(重心は★マークで表示しています)
2・各点について計算された重心からの距離を測り、距離が一番近いグループに割り当て直します。
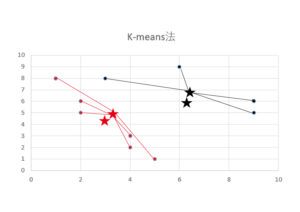
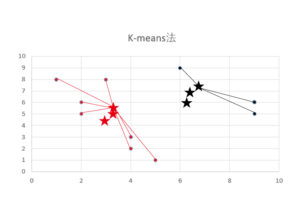
その後、グループが変化しなくなるまで、1と2を何度も繰り返します。
このようにグループが分けられます。
乱数とシードの関係
(ちょっと話が横道にそれますが)
シードはコンピュータ上で乱数を発生させるもとにもなっています。
たとえばコンピュータが10個のデータから5個のデータをランダムに選ぶとします。
シードを1に設定すると1,5,3,4,9が選ばれるとします。
シードを2に設定すれば1,2,8,6,4が選ばれます。
またシードを1に戻すと最初と同じ、1,5,3,4,9が選ばれます。
要するに、コンピュータの乱数はランダムに選ばれているように見えても、実際はシードの設定によって決まっているということですね。
楽曲のプレイリストをシャッフルしてもいつも同じ順番になることが多かったり、ゲームのガチャで連続して当たりが出にくいのもそのためです。
当社のクラスター分析活用方法
話を比階層分析(k-means法)に戻しましょう。
当社では顧客のRFMデータを取り、グループにわけています。
RFMとはRecency (最近の購入日)、Frequency( 来店頻度)、Monetary (購入金額ボリューム)のことです。
RFMを以下のようにランク分けしたとします。
Recency (最近の購入日)
1か月以内は3ポイント
半年以内は2ポイント
1年以上は1ポイント
Frequency( 来店頻度)
100回以上は3ポイント
50回以上100回未満は2ポイント
50回未満は1ポイント
Monetary (購入金額ボリューム)
購入総額30万円以上は3ポイント
10万円以上は2ポイント
10万円未満は1ポイント
RFMともに数値が高いほど、売り上げに貢献しているということが言えますね。
実際はもっと細かく設定することとなりますが、わかれたクラスターごとにグループすると以下のようなグループがいくつもできます。
- 来店頻度が高く、キャンペーン反応も高い層
- 来店頻度は低いが、購入金額が大きい層
- 最近利用をはじめたが購入金額は低い層
- ・・・
- ・・・
- ・・・
- ・・・
- ・・・
- ・・・
- ・・・
皆さんならこの分析結果をどのように活用しますか?
今月はあるグループのお客様にだけ提案するキャンペーン。
来月は幅広いグループのお客様に提案するキャンペーンと分けることも可能です。
グループにあわせたキャンペーン提案など、それぞれに適したアプローチを効率よくかけることで、投資に対する費用対効果を上げることができます。
次元圧縮
ここまでは当社でのクラスター分析活用方法を説明しました。
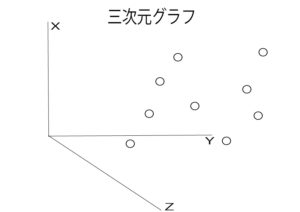
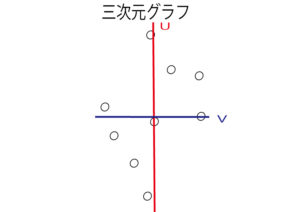
さきほどのRFMをグラフ化すると以下のような3次元散布図が出来上がります。
2次元(縦×横)のグラフと比べて、3次元(縦×横×高さ)の立体的なグラフは視覚的にわかりにくいですよね。
グラフが4次元、5次元と高次元になればなるほど、分析が難しくなるものです。
そもそもクラスター分析自体が近いグループにわけることが目的ですので、2次元や1次元のわかりやすいグラフにするべきではないでしょうか。
次元圧縮(情報を減らす)という方法を使って、3次元グラフを2次元や1次元に変換しましょう。
ここでは3次元から2次元に変換することとします。
次元圧縮する(情報を減らす)場合には主成分分析を使います。
主成分分析
主成分分析とは何かというと、クラスターはどういう根拠で作られたのか調べたり、次元圧縮の結果、失う情報量が最も少なくなるようにする為に行う分析です。
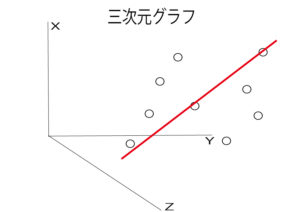
もう一度、さきほどの3次元のグラフを見ましょう。
全ての点から一番近いところに赤い線を引きます。
この赤い線が第1主成分というものです。
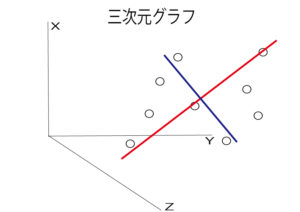
それに対して垂直に引いた線を第2主成分と言います。
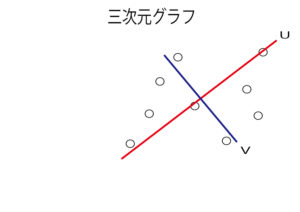
つまり、第1主成分の線をu、第2主成分の線をvとして書いたグラフが、3次元から2次元に次元圧縮したグラフになります。
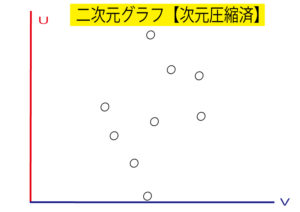
第一主成分uが縦線、第二主成分vが横線になるまで赤線、青線を軸に点を回転させてみましょう。
第一主成分uを左端に、第二主成分vを下に移動させます。
これで次元圧縮した二次元グラフの完成です!
つまり、次元を減らしても、失う情報量が最も少なくなるようにしたグラフができあがったのです。
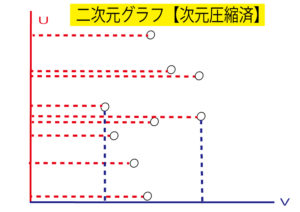
各点からuとvに垂直な線をひいてみましょう。
ここで重要なのは、第一主成分である縦線uのほうがバラツキの多いグラフを作ること。
vはuよりバラツキが少なければOKです。
第1主成分uのばらつきが小さいと情報が欠損してしまいます。
次元圧縮を行ったときに、uの分散(バラツキ)が大きくなるような軸を求めることを主成分分析と言うのです。
ここまでがクラスター分析のお話でした。
ポイントはk-means法と次元圧縮と主成分分析ですね。
おわかりいただけたでしょうか。
当社では機械学習を用いたクラスタリングを
・numpy (数値計算のライブラリ)
・Pandas(データ解析を支援するライブラリ)
・Matplotlib(グラフを描くライブラリ)
・scikitlearn(クラスタリング、回帰、次元削減、分類に使うライブラリ集)
を使って行います。
「当店も顧客をグループ分けして、販促の投資回収率を上げたい」
「商品構成分析をしたい」
「話だけ聞いてみたい」
という方はビデオサービスZOOMを使って20分の無料コンサルをすることができますので、是非ホームページのCONTACTページからお問い合わせください
(通常コンサルは30分5,000円です)。
小平でホームページ制作、経営コンサルティング
mocal design 佐藤 大樹
東京都小平市南町1-27-10
✉ info@ofb.jp
☟トップページはこちらから